Robot3D printsAIC++GamedevLinuxProjectsIdeasDevlogSlotsVlogAbout
Published: Updated:

In this post we collect known research about Artificial Neural Networks and their property to approximate non-linear functions and logical statements. We review simple examples, and in the end we implement Reinforcement Learning purely as a Neural Network.

ANN are universal function approximators

Julien Pascal mentioning the theorem and writing code in Julia

This is our first step that carries important hypotesis that any algorithm can be approximated by Neural Networks.

But before we start, one word from our guest star, Mathuccino.

My advice is don't focus too much on articles

@mathuccino

So practice, practice, practice! We focus on examples implemented with PyTorch and also very transparent version without any ML framework.

Backpropagation formally introduced

The simpliest ANN

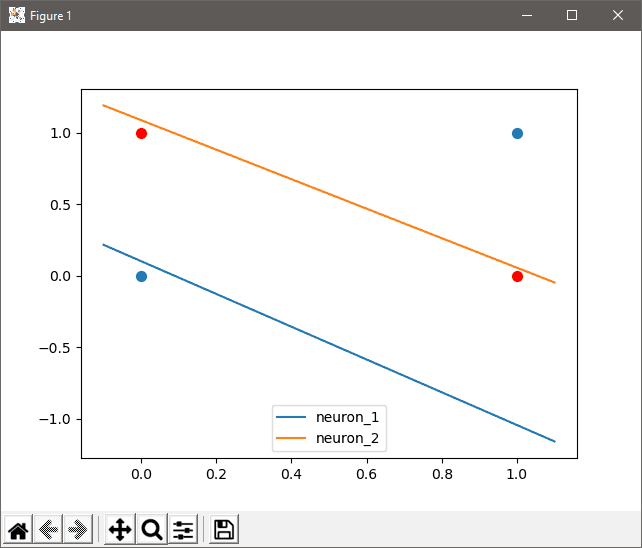
First of all lets create the simpliest but non trivial perceptron - neuron system that works as a XOR function. Two input neurons, two in the hidden layer, and one neuron - output. Simple as that:

Pytorch

import torch
import torch.nn as nn

epochs = 2001
X = torch.Tensor([ [0,0], [0,1], [1,0], [1,1] ])
Y = torch.Tensor([0,1,1,0]).view(-1,1)


class XOR(nn.Module):
    def __init__(self, input_dim = 2, output_dim=1):
        super(XOR, self).__init__()
        self.linear1 = nn.Linear(input_dim, 2)
        self.linear2 = nn.Linear(2, output_dim)
    
    def forward(self, x):
        x = self.linear1(x)
        x = torch.sigmoid(x)
        x = self.linear2(x)
        return x


def train(model):
    # initialize the weight tensor and bias
    linear_layers = [m for m in model.modules() if isinstance(m, nn.Linear)]
    for m in linear_layers:
        # here we use a normal distribution
        m.weight.data.normal_(0, 1)

    mseloss = nn.MSELoss() # mean squared error
    optimizer = torch.optim.SGD(model.parameters(), lr=0.02, momentum=0.9)

    for i in range(epochs):
        y_hat = model.forward(X)
        loss = mseloss(y_hat, Y)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()

Full code (plotting function is skipped for clarity)

Output

I have a problem with 2000 epochs on some seed values. This might give an answer.

Keras

from keras.layers import Dense
from keras.models import Sequential
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt

X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([0, 1, 1, 0])


model = Sequential()
model.add(Dense(1, input_shape=(2,), activation='sigmoid'))
model.compile('adam', 'binary_crossentropy', metrics=['accuracy'])
history = model.fit(X, Y, verbose=1, epochs=20)

Tensorflow (no Keras)

Start with the official docs

No frameworks

So if you think library for machine learning is not making this example any simpler, then look how it would look with no external libraries (only numpy for matrix operations don't know numpy - help!)

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-1 * x))

def relu(x):
    return max(0, x)

epochs = 3000
learning_rate = 0.1
data_inputs = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
data_outputs = np.array([0, 1, 1, 0])
n_neurons_per_layer = [data_inputs.shape[1], 2, 1]

weights_1 = np.random.randn(n_neurons_per_layer[0], n_neurons_per_layer[1]) * 0.1
weights_2 = np.random.randn(n_neurons_per_layer[1], n_neurons_per_layer[2]) * 0.1
bias_1 = np.zeros((1, n_neurons_per_layer[1]))
bias_2 = np.zeros((1, n_neurons_per_layer[2]))

for i in range(epochs):
    n_training_steps = data_inputs.shape[0]
    for idx in range(n_training_steps):
        x = data_inputs[idx, :]
        y = data_outputs[idx] # scalar
        
        x = x[:, np.newaxis].T # column vector
        # first hidden layer
        y_1 = np.dot(x, weights_1) + bias_1 # why x is first? (bias - column vector)
        y_1 = sigmoid(y_1) # column vector
        # output
        y_2 = np.dot(y_1, weights_2) + bias_2 # column vector (just one row)
        # y_2 = sigmoid(y_2)
        y_2 = relu(y_2)
        
        diff = y - y_2 # 1 element matrix (column vector)
        
        grad_2 = 1 # y_2 * (1 - y_2) # sigmoid derivative
        d_2 = diff * grad_2 # 1 element matrix (column vector)
        # np.sum(dZ2,axis=1,keepdims=True)
        dw2 = y_1.T.dot(d_2)
        weights_2 += learning_rate * dw2
        bias_2 += learning_rate * d_2
        
        grad_1 = y_1 * (1 - y_1) # sigmoid derivative
        d_1 = (weights_2.T * d_2) * grad_1
        dw1 = x.T.dot(d_1)
        weights_1 += learning_rate * dw1
        bias_1 += learning_rate * d_1

def network_forward(x):
    global weights_1, weights_2, bias_1, bias_2
    y_1 = np.dot(x, weights_1) + bias_1
    y_1 = sigmoid(y_1)
    y_2 = np.dot(y_1, weights_2) + bias_2
    y_2 = relu(y_2)
    if isinstance(y_2, np.ndarray):
        y_2 = y_2.item()
    return y_2

print(network_forward(np.array([0,0])))
print(network_forward(np.array([0,1])))
print(network_forward(np.array([1,0])))
print(network_forward(np.array([1,1])))

Later you might be tempted to review such simple systems further

  • The simplest artificial neural network possible explained and demonstrated. Even if you don't code in Go, check out the theory - it's the "bone structure" you need to understand. Better matrix pictures
  • But if in the first place you want math stuff, then here is a simple explanation, or about gradients, or this chapter from free book.
  • Machine-learning-without-any-libraries repo is designed to teach Machine Learning without any framework, no external dependencies (actually it requires: numpy, pandas, scikit-learn, matplotlib). In this example ANN has one hidden layer, tanh and sigmoid functions for activation, and backpropagation as learning algorithm. But it has wrong gradient for the output neuron. The way how functions pass values is far from readability, data loading can be orginized better, together with plotting functions it can eliminate all extra dependencies when only numpy will remain.
  • Another NumPy only version. My mistake, I started fiddling with ANN implementations by taking this code first. It doesn't have biases, no backpropagation, and no gradient descent in particular. Don't repeat my mistake.
  • I don't know why all these examples are similar, like copied one from another without thinking, but this article and code can be a good starting point. Someone tried to orginize code in small functions with some flexibility in mind. This and very space-y coding style make it hard to read. Take a look on the cache carried between forward and backward passes - it's very important concept for efficient implementation.
  • In case you want to see how it can be orginized in classes, then here's another post on Medium
  • To do it clearly with no libraries, check out unbeatable and legendary Jason Brownlee here. He has some explanation about backpropaganation to the hidden layer (about multiplication on the weight matrix).
  • ANN Primer for Neuroscientists. It covers the mathematical foundational aspects as well as the code for "hands on" experience. Around 30 examples are in the repo (written for Tensorflow 1.8.0, Python 2.7 / 3.6)
  • Why cross-entropy better than mean squared error (better converges to 0 1 limits if we are using softmax on output)
  • Play with another cost functions

Function approximation

Then let's approximate the sin function and generalize our knowledge for any function. What requirements stand for functions in order to be approximable by neural networks?

Later we will focus out research on aspects such as

  • function sophistication (hypothesis: you get an excellent approximation but with apparently many more epochs needed)
  • function properties: differentiable, continuous, smooth
  • sinusoid and exponential (infinitely differentiable so no problems) -> approx with linear regression
  • structural limitations of the network
  • accuracy control

Here is a blog post which tackles a few of the last bullet points.

3d function approximation

This post tries to explain how artificial neural networks work. So it is not about the algebraic part. Instead it tries to answer why size and structure matter, how the activation function makes a difference. And there I found the mesh neural networks interesting.

Numerical differentiation

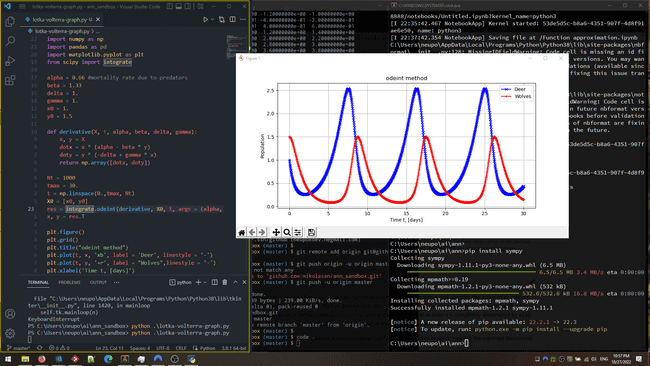
Lotka Volterra model

Theory and graphs

So I'm trying to find Python library for numerical differentiation. numpy should do it, but I don't see an example for function of two variables f(x, y) that depend on time - x(t), y(t).

For the multivariable thing you don't use numpy but SymPy. A more digestible tuto. It also explains how to use the chain rule

For Lotka-Volterra ordinary differential equations

Lotka Volterra graph

Logic statements in ANN

I've found two articles, more of a good read than a coding tutorial, it seems relevant:

  1. Emulating logical gates with a neural network
  2. How to teach logic to your neural networks. And in this last link, you will find a link to TensorFlow Playground, that could help you visualize your network. And the associated GitHub page

Develop new actions

If it uses fixed model of states and actions then it's not good. Is there a model that can develop new actions and adapt to the environment?

I worked on adaptive algos for my med internship. it's the natural extension of ANNs apparently when coupled with the neural network approach

A man-made adaptive neural network, also called an artificial neural network, is modeled after the naturally occurring neural networks in the brains of humans and animals.

It's the same thing as an ANN pretty much

Ok so the main use is for a single-layer algo. It's called Adaline if you want

Seems like a good start before having to deal with 5364 layers

Activity Recognition with Adaptive Neural Networks - Notebook and paper

Multi Layer Perceptron - I don't like this approach too much but just sending in case

I think conventional "training" is wrong because it stops once errors on test set are minimized which obviously reveals the flaw - the network can only do what it trained to do), but I see that ANN can approximate functions, can follow logical statements, can store information as memory. It creates a base for my theory. Some insights can be borrowed from neuroscience to advance ANN quality, but there must be a way to transfer connections into symbolism - extract functions, logic and memories encoded in ANN. So what we just did, but in reverse.

Bonus reading

This repo simulates a car that mustn't touch walls. "A 2D Unity simulation in which cars learn to navigate themselves through different courses. The cars are steered by a feedforward neural network. The weights of the network are trained using a modified genetic algorithm." Cars on C# is basically a "game" made on Unity game engine - hard to use as a standalone project. It was created 6 years ago - may be problems to run it on current Unity version. Also training by genetic algorithm is no go. The result is cool tho. (Unity, Genetic algorithm)

Neural Network Zoo and a prequel by Fjodor van Veen

Just another Python library - PyGAD. It's focused on optimization algorithms and genetic algorithms. Specifically ANN module can be interesting in regards the current topic.

Best notation

  1. Ostwald 2021
  2. Neilsen's book
  3. Wiedemann 2020
  4. Xiong 2022
  5. Wang 2021

Rate this page